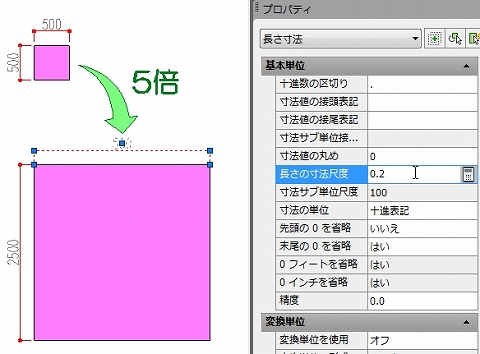
前回は、モデル空間内で異なる縮尺の図面を表示させる場合の基本的な考え方を、もう一度詳しく説明しました。
縮尺1/100の図面に縮尺1/5の図面を入れる場合にどうしたら良いか、という話でした。
ちょっと面倒な感じのする概念ですが、ここで理解しておけば、ペーパー空間を理解する際にも役立ちます。
多少の時間をかけてでも、ぜひこの縮尺の考え方を自分の知識としておくことをお勧めします。
それを人に説明するようなチャンスがあれば、自分の知識も整理されて都合がいいんですけど……
私の説明があまり分かりやすくないので、そんなことを言ってもあまり説得力がないですね。
それでも、もう少しだけ話を続けることにして、今回の例ではなぜ拡大図を20倍にしたのかについて考えてみたいと思います。
■拡大率の計算方法
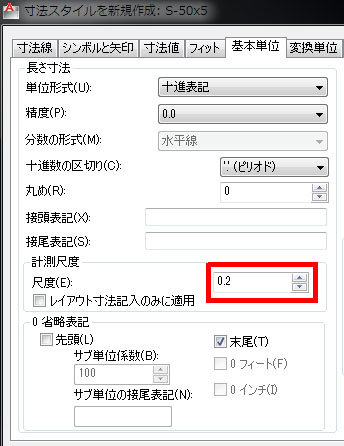
縮尺1/100の図面に縮尺1/5の図面を入れる場合、1/5で表示したい要素を20倍にしておく必要があります。
ここで唐突に20倍という数値が出てくる訳ですが、この数値は一体どこから登場してきたのか。
これを理解しておけば、縮尺1/50の図面に縮尺1/3の図面を入れるなど、数値が変わっても応用がききます。
ということで、ここでその計算方法と考え方を書いてみますが、結局は前回説明した話と同じなんですよね。
見るポイントはそれぞれの縮尺と、結局はどちらの縮尺に合わせて印刷をするのかという部分。
今回で言えばこうなります。
・モデル空間で印刷する際の縮尺:1/100(A)
・拡大図で表現したい縮尺:1/5(B)
・拡大図を拡大縮小する倍率:20倍(X)
具体的な数値はあくまでも今回の例だけの話なので、上記の一番右にある記号で計算式を作ると……
X=B/A
ということになります。
■計算式の考え方
これをもう少し分かりやすく表現すると、こんな感じで考えていけば良いんじゃないかと思います。
あらかじめ拡大しておいた詳細図を、モデル空間で一緒に表現する図面の縮尺で縮小すると、目的の縮尺になるから……
↓
拡大する倍率(X)×印刷時の縮小率(A)=実際に見せたい縮尺(B)
↓
拡大する倍率(X)=実際に見せたい縮尺(B)/印刷時の縮小率(A)
↓
X=B/A
↓
今回の場合は X=(1/5)/(1/100)
↓
分数の割り算は逆数になるので X=(1/5)×100=20
という計算になります。
拡大図の倍率とモデル空間で印刷する場合の縮尺、そして最終的に図面として見せたい縮尺。
これらの関係が理解できれば、計算自体はもの凄くシンプルですから、困ることはなくなります。
慣れてくると縮尺の分母だけで「100/5=20」と計算出来るようになりますが、その為には基本概念の理解が必要になります。
まずはこの考え方をしっかりと押さえておくことをお勧めします。